/Szkoła średnia/Ciągi/Arytmetyczny/Czterowyrazowy

Zadanie nr 5814751

Dla pewnych liczb 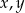x,y wartości wyrażeń 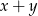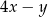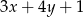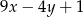x + y , 4x − y , 3x + 4y + 1 , 9x − 4y + 1 są początkowymi, kolejnymi wyrazami ciągu arytmetycznego. Oblicz, ile początkowych wyrazów tego ciągu należy wziąć, aby ich suma była większa od 20100.

Wersja PDF

Rozwiązanie

W ciągu arytmetycznym różnice kolejnych wyrazów są stałe, zatem

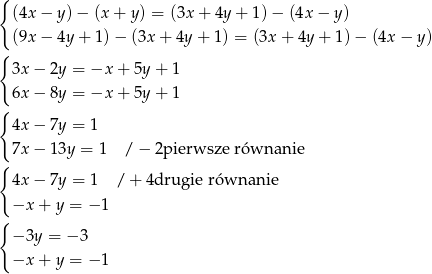
{ (4x − y) − (x + y ) = (3x+ 4y + 1) − (4x − y) (9x − 4y + 1 )− (3x + 4y+ 1) = (3x + 4y + 1) − (4x − y ) { 3x − 2y = −x + 5y + 1 6x − 8y = −x + 5y + 1 { 4x − 7y = 1 7x − 13y = 1 / − 2pierwsze równanie { 4x − 7y = 1 / + 4drugie równanie −x + y = − 1 { − 3y = −3 −x + y = − 1

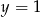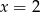Stąd y = 1 i x = 2 i dany ciąg to 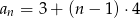an = 3 + (n − 1) ⋅4 . Musimy rozwiązać nierówność

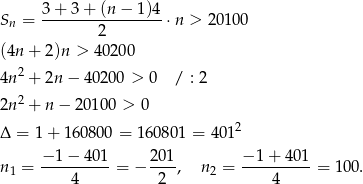
3+ 3+ (n − 1)4 Sn = -----------------⋅n > 2 0100 2 (4n + 2)n > 4020 0 4n 2 + 2n − 40200 > 0 / : 2 2n 2 + n − 2 0100 > 0 2 Δ = 1+ 16080 0 = 16080 1 = 401 −-1−--401- 201- −-1-+-401- n1 = 4 = − 2 , n 2 = 4 = 100.

Zatem 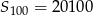S100 = 201 00 . Musimy zatem wziąć co najmniej 101 wyrazów.  
Odpowiedź: Co najmniej 101 wyrazów

Wersja PDF