Zadanie nr 9352499
Wyznacz współrzędne punktu przecięcia się przekątnych czworokąta 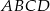 jeżeli
jeżeli 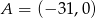 ,
, 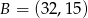 ,
, 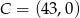 i
i 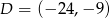 .
.
Rozwiązanie
Ponieważ punkty 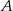 i
i 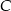 leżą na osi
leżą na osi 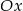 , więc przekątna
, więc przekątna 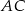 danego czworokąta pokrywa się z osią
danego czworokąta pokrywa się z osią 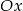 .
.
Napiszemy teraz równanie przekątnej 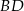 . Szukamy prostej w postaci
. Szukamy prostej w postaci 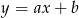 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 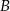 i
i 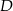 .
.
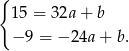
Odejmujemy od pierwszego równania drugie (żeby skrócić 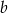 ) i mamy
) i mamy
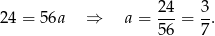
Mamy stąd 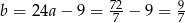 i prosta
i prosta 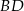 ma równanie
ma równanie 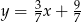 . Pozostało teraz wyznaczyć pierwszą współrzędną punktu wspólnego tej prostej z osią
. Pozostało teraz wyznaczyć pierwszą współrzędną punktu wspólnego tej prostej z osią 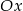 (czyli z przekątną
(czyli z przekątną 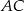 ).
).
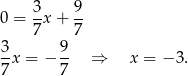
Odpowiedź: