/Studia/Analiza/Ciągi/Granice/Z kropkami

Zadanie nr 3331753

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz granicę 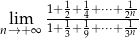1+ 1+1+ ⋅⋅⋅+ 1n- lim 1+-21+41+-⋅⋅⋅+-21- n→ +∞ 3 9 3n .

Rozwiązanie

Sposób I

Korzystamy ze wzoru na sumę ciągu geometrycznego.

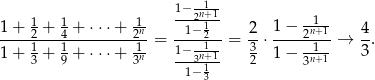
1− -1-- 1 + 1+ 1+ ⋅⋅⋅+ 1- ---2n+11- 1− -1-- -----2---4---------2n-= --1−2-- = 2-⋅ ----2n+-1→ 4. 1 + 13 + 19 + ⋅⋅⋅+ 13n- 1−-31n+1- 32 1− 31n+-1 3 1−13

Sposób II

Ponieważ zarówno w mianowniku jak i w liczniku mamy zbieżne szeregi geometryczne, granica ich ilorazu to iloraz granic, czyli (ze wzoru na sumę szeregu geometrycznego).

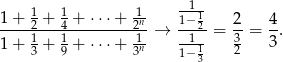
1 1 1- -1-1 1+--2 +-4-+-⋅⋅⋅+--2n-→ 1−-2 = -2 = 4-. 1+ 13 + 19 + ⋅⋅⋅+ 13n -1-1 32 3 1− 3

 
Odpowiedź: 43

Wersja PDF