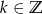/Studia/Analiza/Ciągi/Granice/Z kropkami

Zadanie nr 9226951

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 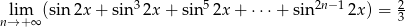3 5 2n−1 2 nl→im+∞ (sin 2x + sin 2x + sin 2x + ⋅ ⋅⋅+ sin 2x) = 3 .

Rozwiązanie

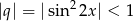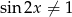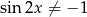Lewa strona to po prostu, trochę nietypowo zapisana, suma szeregu geometrycznego będącego w nawiasie. Szereg ten jest zbieżny o ile |q| = |sin22x | < 1 , czyli dla sin 2x ⁄= 1 i sin2x ⁄= − 1 . Mamy wtedy

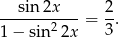
--sin-2x---= 2-. 1 − sin22x 3

Podstawiając 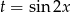t = sin 2x mamy

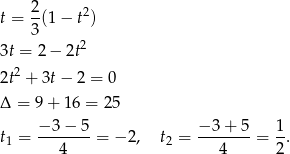
t = 2-(1− t2) 3 3t = 2 − 2t2 2t2 + 3t− 2 = 0 Δ = 9 + 16 = 25 −-3-−-5 −-3-+-5 1- t1 = 4 = − 2, t2 = 4 = 2.

Zatem

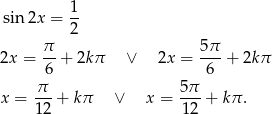
sin 2x = 1- 2 π- 5π- 2x = 6 + 2kπ ∨ 2x = 6 + 2kπ π 5π x = ---+ k π ∨ x = ---+ kπ . 12 12

 
Odpowiedź: 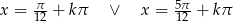π 5π x = 12 + kπ ∨ x = 12-+ kπ dla k ∈ Z

Wersja PDF