Udowodnij że jeśli dwie dwusieczne w trójkącie są sobie równe to trójkąt jest równoramienny (twierdzenie Steinera-Lehmusa).
/Konkursy/Zadania/Geometria/Planimetria/Trójkąt/Dwusieczne
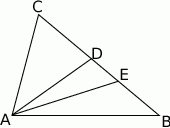
Dwusieczna kąta 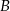 trójkąta
trójkąta 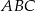 przecina bok
przecina bok 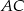 w punkcie
w punkcie 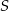 , a dwusieczna kąta
, a dwusieczna kąta 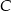 przecina bok
przecina bok 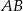 w punkcie
w punkcie 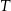 . Dwusieczne przecinają się w punkcie
. Dwusieczne przecinają się w punkcie 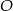 . Znajdź miarę kąta
. Znajdź miarę kąta 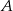 , jeżeli wiadomo, że na czworokącie
, jeżeli wiadomo, że na czworokącie 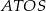 można opisać okrąg.
można opisać okrąg.
W trójkącie 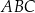 dwusieczna kąta
dwusieczna kąta 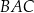 przecina bok
przecina bok 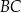 trójkąta w punkcie
trójkąta w punkcie 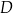 . Wykaż, że
. Wykaż, że
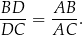
W trójkacie 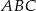 dwusieczna kąta
dwusieczna kąta 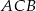 przecina bok
przecina bok 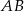 w punkcie
w punkcie 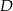 . Długosci boków
. Długosci boków 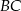 i
i 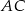 są równe odpowiednio
są równe odpowiednio  i
i 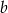 , a długość odcinka
, a długość odcinka 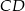 jest równa
jest równa 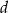 . Wykaż, że
. Wykaż, że 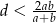 .
.
Na boku 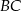 trójkąta
trójkąta 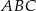 wybrano punkt
wybrano punkt 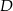 tak, by
tak, by 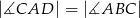 . Odcinek
. Odcinek 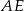 jest dwusieczną kąta
jest dwusieczną kąta 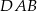 . Udowodnij, że
. Udowodnij, że 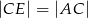 .
.