/Szkoła podstawowa/Geometria/Figury przestrzenne/Prostopadłościan

Zadanie nr 2159805

Dodaj do ulubionych
Dodaj do rozwiązanych

Objętość prostopadłościanu jest równa 405. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1 : 3 : 5. Oblicz pole powierzchni całkowitej prostopadłościanu.

Rozwiązanie

Oznaczmy długości krawędzi prostopadłościanu przez 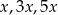x,3x ,5x .

PIC

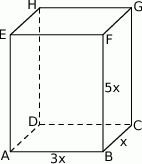
Z podanej informacji o objętości mamy równanie

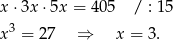
x ⋅3x ⋅5x = 405 / : 15 x3 = 2 7 ⇒ x = 3.

Obliczamy teraz pole powierzchni prostopadłościanu.

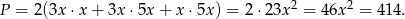
2 2 P = 2(3x ⋅x + 3x ⋅5x + x ⋅5x ) = 2⋅2 3x = 46x = 414.

 
Odpowiedź: 414

Wersja PDF