/Studia/Algebra liniowa/Przestrzenie liniowe

Zadanie nr 6628835

Czy zbiór 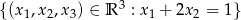3 {(x1,x2,x3) ∈ R : x1 + 2x2 = 1 } jest podprzestrzenią linową R 3 ?

Wersja PDF

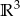Rozwiązanie

Musimy sprawdzić czy podany zbiór 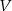V jest zamknięty ze względu na sumę wektorów:

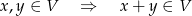
x,y ∈ V ⇒ x + y ∈ V

oraz na mnożenie przez skalar:

a ∈ R ,x ∈ V ⇒ ax ∈ V .

Jeżeli zaczniemy sprawdzać te warunki, to nam nie wyjdzie (przez 1 z prawej strony). Pokażmy zatem, że ten zbiór nie jest podprzestrzenią liniową. Nie jest to trudne, wystarczy pokazać przykład, że zbiór ten nie jest zamknięty na sumę lub mnożenie przez skalar.

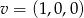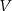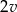Możemy np. wziąć v = (1,0,0) . Ten wektor należy do V , ale 2v już nie należy.  
Odpowiedź: Nie, nie jest.

Wersja PDF