Zadanie nr 1697767
Oblicz całkę 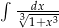 .
.
Rozwiązanie
Ponieważ
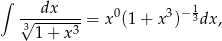
więc mamy do czynienia z różniczką dwumienną postaci
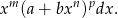
W naszej sytuacji mamy
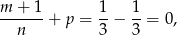
więc możemy podstawić 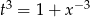 (jest to ogólna metoda całkowania różniczek dwumiennych). Mamy wtedy
(jest to ogólna metoda całkowania różniczek dwumiennych). Mamy wtedy
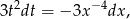
oraz
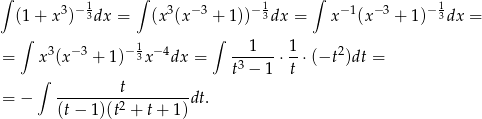
Rozkładamy teraz wyrażenie podcałkowe na ułamki proste
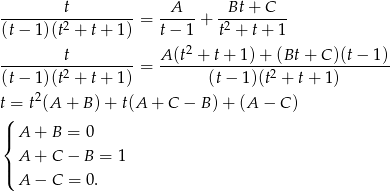
Łatwo stąd otrzymać, że 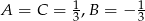 . Mamy więc
. Mamy więc
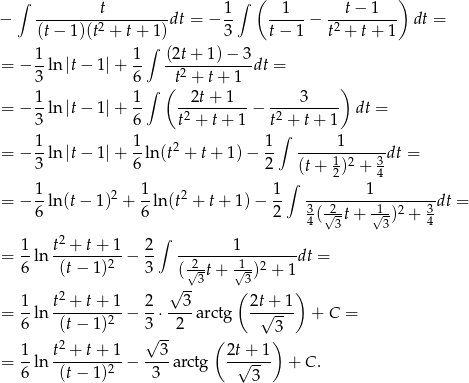
Odpowiedź: 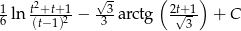 , gdzie
, gdzie