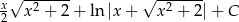Zadanie nr 2998892
Oblicz całkę 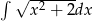 .
.
Rozwiązanie
Sposób I
Podstawmy 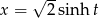 . Mamy wtedy
. Mamy wtedy
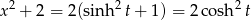
oraz
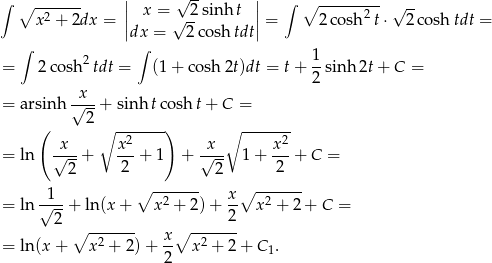
Sposób II
Stosujemy I podstawienie Eulera 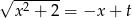 .
.
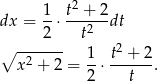
Mamy zatem
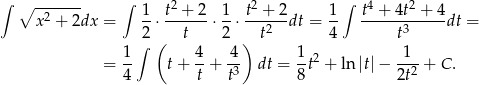
Zanim przekształcimy to wyrażenie dalej, obliczmy 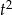 i
i 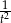 .
.
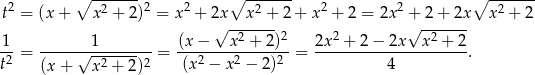
Mamy więc
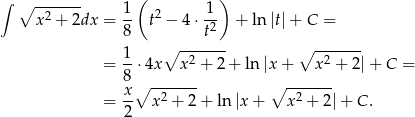
Sposób III
Tym razem skorzystamy ze wzoru
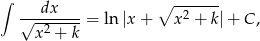
który można wyprowadzić używając I podstawienia Eulera.
Przekształcimy teraz szukaną całkę na dwa sposoby: pierwszy to całkowanie przez części, a w drugim przeniesiemy pierwiastek do mianownika.
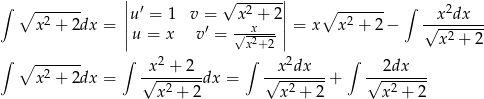
Dodając te dwie równości stronami mamy
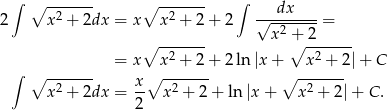
Odpowiedź: