Zadanie nr 3623310
Oblicz całkę 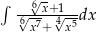 .
.
Rozwiązanie
Podstawiamy 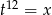 .
.
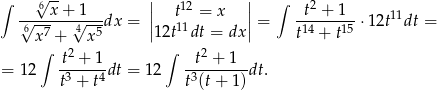
Szukamy teraz rozkładu na ułamki proste
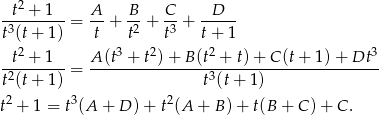
Patrząc na wyrazy wolne mamy 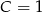 , skąd
, skąd 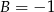 ,
, 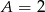 oraz
oraz 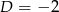 . Mamy więc
. Mamy więc
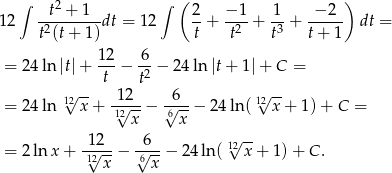
Odpowiedź: 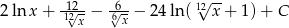
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 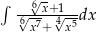 .
.
Podstawiamy 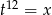 .
.
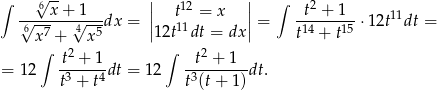
Szukamy teraz rozkładu na ułamki proste
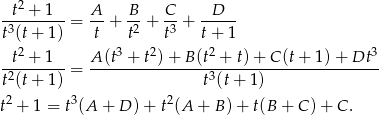
Patrząc na wyrazy wolne mamy 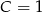 , skąd
, skąd 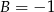 ,
, 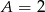 oraz
oraz 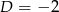 . Mamy więc
. Mamy więc
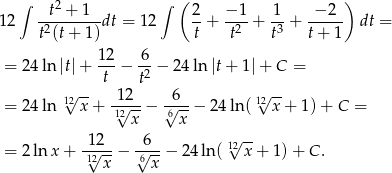
Odpowiedź: