Zadanie nr 4548232
Oblicz całkę 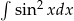 .
.
Rozwiązanie
Sposób I
Najprostszy sposób policzenia tej całki, to skorzystanie ze wzoru
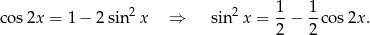
Liczymy
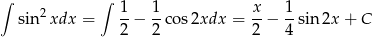
Sposób II
Jeżeli ktoś nie lubi tożsamości trygonometrycznych, to może całkować przez części.
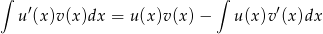
Liczymy
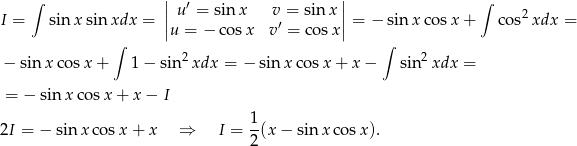
Odpowiedź: 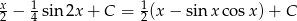
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 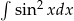 .
.
Sposób I
Najprostszy sposób policzenia tej całki, to skorzystanie ze wzoru
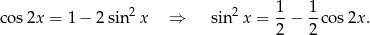
Liczymy
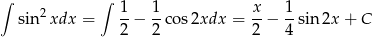
Sposób II
Jeżeli ktoś nie lubi tożsamości trygonometrycznych, to może całkować przez części.
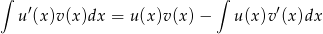
Liczymy
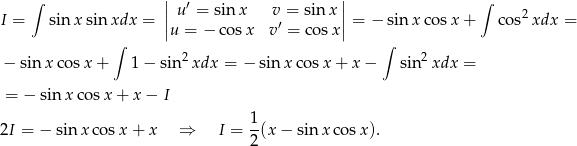
Odpowiedź: