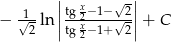Zadanie nr 5302372
Oblicz całkę 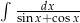 .
.
Rozwiązanie
Stosujemy podstawienie uniwersalne 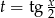 .
.
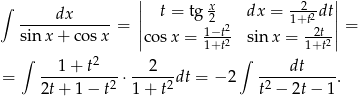
Ostatnią całkę obliczamy korzystając z rozkładu na ułamki proste.
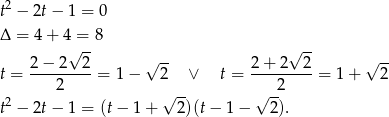
Łatwo teraz zgadnąć rozkład na ułamki proste
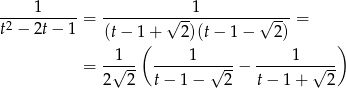
Zatem
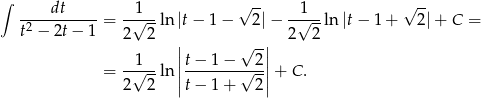
Mamy więc
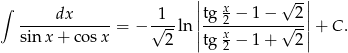
Odpowiedź: 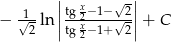
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 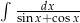 .
.
Stosujemy podstawienie uniwersalne 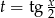 .
.
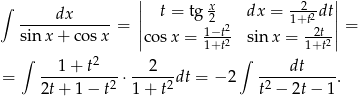
Ostatnią całkę obliczamy korzystając z rozkładu na ułamki proste.
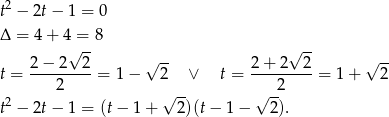
Łatwo teraz zgadnąć rozkład na ułamki proste
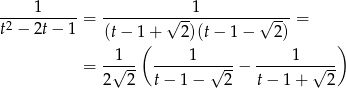
Zatem
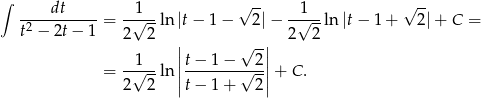
Mamy więc
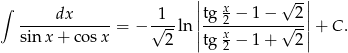
Odpowiedź: