Zadanie nr 7559485
Oblicz całkę 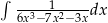 .
.
Rozwiązanie
Mianownik dzieli się przez  :
:
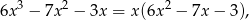
a dwumian kwadratowy 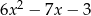 ma dwa pierwiastki
ma dwa pierwiastki
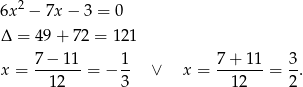
Mamy rozkład
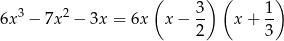
i funkcja podcałkowa jest sumą trzech ułamków prostych pierwszego rodzaju:
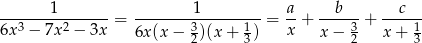
Mnożymy obie strony przez 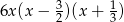 .
.
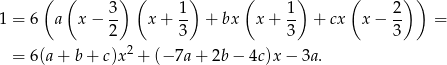
Porównując współczynniki otrzymujemy układ równań.
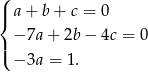
Z ostatniego równania mamy 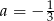 , a odejmując od drugiego równania pierwsze pomnożone przez 2 (żeby zredukować
, a odejmując od drugiego równania pierwsze pomnożone przez 2 (żeby zredukować 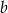 ) mamy
) mamy
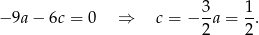
Zatem
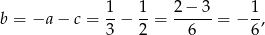
oraz
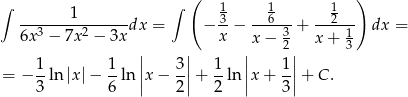
Odpowiedź: