/Studia/Analiza/Całki nieoznaczone

Zadanie nr 9185055

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 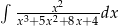∫ -----x2------ x3+ 5x2+ 8x+4dx .

Rozwiązanie

Najpierw musimy rozłożyć mianownik na czynniki liniowe lub kwadratowe. W tym celu musimy odgadnąć jeden jego pierwiastek. Łatwo sprawdzić podstawiając, że 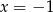x = − 1 jest pierwiastkiem mianownika, zatem wielomian ten dzieli się przez 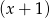(x + 1) . My jak zwykle zrobimy to grupując wyrazy.

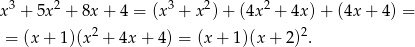
x3 + 5x2 + 8x + 4 = (x3 + x2) + (4x 2 + 4x )+ (4x+ 4) = 2 2 = (x+ 1)(x + 4x + 4) = (x + 1 )(x+ 2) .

Zatem

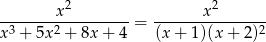
2 2 -------x----------= ------x--------- x3 + 5x2 + 8x + 4 (x + 1)(x + 2)2

i funkcja wymierna jest więc sumą trzech ułamków prostych pierwszego rodzaju:

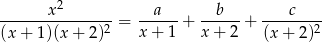
x2 a b c --------------2-= ------+ ------+ -------2- (x + 1)(x + 2) x + 1 x + 2 (x + 2)

Mnożąc obie strony przez 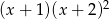2 (x+ 1)(x+ 2) otrzymujemy

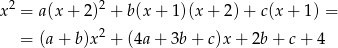
2 2 x = a(x + 2) + b(x + 1 )(x + 2)+ c(x + 1 ) = = (a + b)x2 + (4a + 3b + c)x + 2b + c + 4

Porównując współczynniki przy kolejnych potęgach x otrzymujemy układ równań.

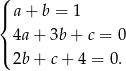
( |{ a + b = 1 4a + 3b + c = 0 |( 2b + c + 4 = 0 .

Zostawiając pierwsze równanie i odejmując od drugiego równania trzecie (żeby zredukować c ) otrzymujemy

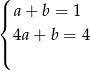
( |{ a+ b = 1 4a+ b = 4 |(

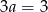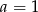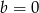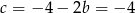Odejmujemy teraz od drugiego równania pierwsze i mammy 3a = 3 , czyli a = 1 . Stąd b = 0 i c = −4 − 2b = − 4 .

Mamy zatem

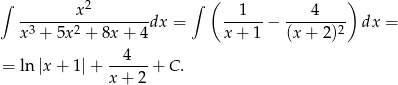
∫ x 2 ∫ ( 1 4 ) -3-----2---------dx = ------− -------2- dx = x + 5x + 8x + 4 x + 1 (x + 2) --4--- = ln |x + 1|+ x+ 2 + C .

 
Odpowiedź: ln |x+ 1|+ -4--+ C x+2

Wersja PDF