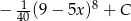/Studia/Analiza/Całki nieoznaczone

Zadanie nr 9265749

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 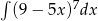∫ 7 (9 − 5x) dx .

Rozwiązanie

Sposób I

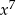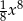Wiemy, że funkcją pierwotną do 7 x jest 1 8 8x , zatem spodziewamy się wyniku postaci 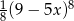18(9 − 5x )8 . Jeżeli policzymy pochodną z tego wyrażenia okaże się, że musimy dodać z przodu współczynnik − 1 5 .

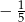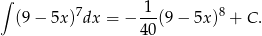
∫ 7 -1- 8 (9 − 5x) dx = − 40 (9− 5x) + C.

Sposób II

Podstawiamy 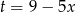t = 9 − 5x .

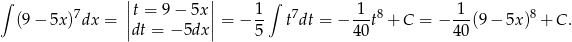
∫ | | ∫ (9− 5x)7dx = ||t = 9 − 5x|| = − 1- t7dt = − -1t8 + C = − 1-(9 − 5x)8 + C. |dt = − 5dx| 5 40 40

 
Odpowiedź: 1 8 − 40(9 − 5x ) + C

Wersja PDF