/Studia/Algebra liniowa/Liniowa niezależność/W przestrzeni funkcji

Zadanie nr 2616397

Czy w przestrzeni funkcji rzeczywistych układ wektorów 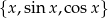{x,sin x,cos x} jest liniowo niezależny?

Wersja PDF

Rozwiązanie

Pokażemy, że ten układ jest liniowo niezależny. Załóżmy, że

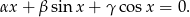
αx + β sinx + γ cos x = 0.

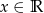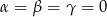Warto podkreślić, że jest to równość w przestrzeni funkcji, czyli jest spełniona dla każdego x ∈ R . Możemy więc podstawiać w tej równości dowolne x – w ten sposób pokażemy, że α = β = γ = 0 . Podstawiając 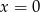x = 0 mamy

γ cos 0 = 0 ⇒ γ = 0.

Zostaje nam więc

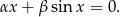
αx + β sin x = 0.

Podstawiając 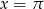x = π mamy

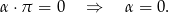
α ⋅π = 0 ⇒ α = 0.

Zostało nam

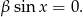
β sinx = 0.

Podstawiając 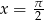π- x = 2 mamy β = 0 .  
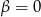Odpowiedź: Układ jest liniowo niezależny.

Wersja PDF