Zadanie nr 3258599
Czy w przestrzeni funkcji rzeczywistych układ wektorów 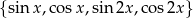 jest liniowo niezależny?
jest liniowo niezależny?
Rozwiązanie
Pokażemy, że ten układ jest liniowo niezależny. Załóżmy, że
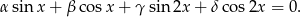
Podstawiając 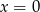 mamy
mamy
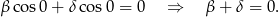
Jeżeli natomiast 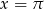 to
to
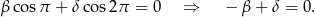
Stąd łatwo wynika, że 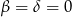 i zostaje nam
i zostaje nam
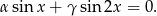
Podstawiając 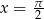 mamy
mamy
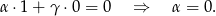
Zostaje
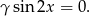
Podstawiając 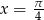 dostajemy
dostajemy 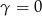 .
.
Odpowiedź: Układ jest liniowo niezależny.

