Niech E będzie dowloną przestrzenią liniową, A niepustym podzbiorem... Zadania.info: rozwiązanie zadania, Abstrakcyjne, 8365716

Forum

Zadanie nr 8365716

Niech 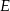$E$ będzie dowloną przestrzenią liniową, 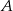$A$ niepustym podzbiorem $E$ .

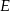Wykazać, że zbiór 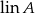$linA$ wszystkich możliwych kombinacji liniowych wektorów ze zbioru 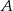$A$ jest podprzestrzenią przestrzeni $E$ .
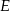Wykazać, że 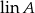$linA$ jest najmniejszą (w sensie inkluzji) podprzestrzenią przestrzeni 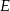$E$ , zawierającą zbiór $A$ .
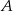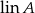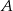Czym jest $lin A$ , gdy $A$ jest podprzestrzenią przestrzeni $E$ ?

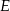Rozwiązanie

Musimy pokazać, że zbiór 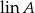$linA$ jest zamknięty ze względu na dodawanie wektorów i na mnożenie ich przez skalar. Jeżeli 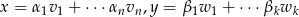$x = α v + ⋅⋅⋅ α v ,y = β w + ⋅⋅ ⋅β w 1 1 n n 1 1 k k$ , gdzie 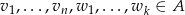$v1,...,vn,w 1,...,wk ∈ A$ , to jest jasne, że 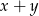$x+ y$ też jest kombinacją wektorów z 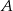$A$ . Taką kombinacją jest też 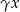$γx$ , dla dowolnego skalara $γ$ .
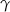Pokazaliśmy już, że 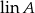$linA$ jest podprzestrzenią, ponadto zawiera ona 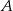$A$ . Niech teraz 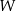$W$ będzie dowolną podprzestrzenią zawierającą 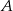$A$ . Wtedy 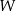$W$ musi zawierać wszystkie kombinacje wektorów z 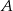$A$ , czyli musi zawierać $linA$ .
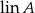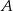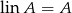Jeżeli $A$ jest podprzestrzenią, to jest zamknięty ze względu na branie kombinacji liniowych, czyli $lin A = A$ .

Twoje uwagi

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!