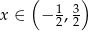/Szkoła średnia/Funkcje/Kwadratowa/Ekstrema

Zadanie nr 1344667

Dodaj do ulubionych
Dodaj do rozwiązanych

Określ zbiór wartości funkcji: 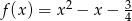2 3 f(x) = x − x− 4 . Dla jakich argumentów funkcja przyjmuje wartości ujemne?

Rozwiązanie

Policzmy najpierw współrzędne wierzchołka paraboli będącej wykresem funkcji 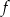f .

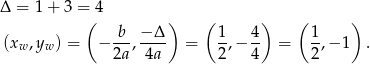
Δ = 1 + 3 =( 4 ) ( ) ( ) b − Δ 1 4 1 (xw ,yw) = − ---,---- = --,− -- = --,−1 . 2a 4a 2 4 2

Ponieważ ramiona paraboli są skierowne do góry, zbiór wartości funkcji 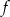f to przedział ⟨− 1,+ ∞ ) .

PIC

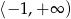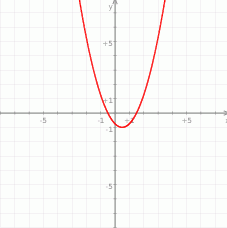
Aby wyznaczyć przedział, na którym funkcja jest ujemna musimy obliczyć jej miejsca zerowe.

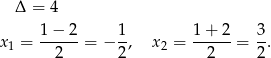
Δ = 4 1 − 2 1 1+ 2 3 x 1 = ------= − -, x2 = ------= -. 2 2 2 2

Funkcja przyjmuje wartości ujemne na przedziale 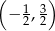( ) − 1, 3 2 2 .  
Odpowiedź: Zbiór wartości: 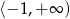⟨− 1,+ ∞ ) , wartości ujemne dla ( ) 1 3 x ∈ − 2,2

Wersja PDF