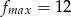/Szkoła średnia/Funkcje/Kwadratowa/Ekstrema

Zadanie nr 1467115

Oblicz najmniejszą i największą wartość funkcji kwadratowej 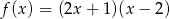f (x) = (2x + 1)(x − 2) w przedziale ⟨− 2,2⟩ .

Wersja PDF

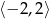Rozwiązanie

Jeżeli zapiszemy funkcję 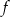f w postaci

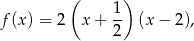
( 1) f(x) = 2 x+ -- (x − 2), 2

to możemy naszkicować jej wykres – ma ona pierwiastki 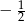1 − 2 i 2 i ramiona skierowane do góry.

PIC

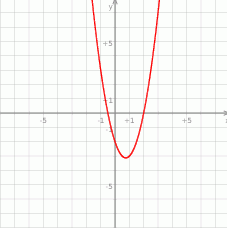
Widać, że wartość najmniejsza jest przyjmowana w wierzchołku paraboli (tu jest ważne, że znajduje się on w przedziale 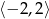⟨− 2 ,2 ⟩ ). Aby znaleźć jego współrzędne przekształćmy podany wzór funkcji

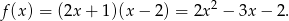
f (x) = (2x + 1)(x − 2) = 2x2 − 3x − 2.

Stąd

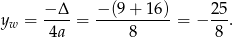
− Δ − (9 + 16) 25 yw = ----= -----------= − --. 4a 8 8

Jeżeli chodzi o wartość największą, to jest ona przyjmowana w jednym z końców przedziału (z rysunku widać, że w lewym, ale na wszelki wypadek to policzmy).

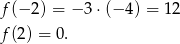
f(− 2) = − 3 ⋅(− 4) = 12 f(2) = 0.

Zatem największa wartość to 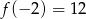f(− 2) = 12 .  
Odpowiedź: 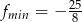f = − 25- min 8 i f = 12 max

Wersja PDF