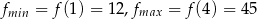Zadanie nr 3651051
Wyznacz największą i najmniejszą wartość funkcji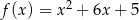 
osiąganą w przedziale 
.
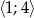Rozwiązanie
Wykresem tej funkcji jest parabola o ramionach skierowanych do góry i wierzchołku w punkcie
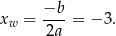
Ponieważ wierzchołek znajduje się na lewo od podanego przedziału, funkcja na tym przedziale jest rosnąca, więc najmniejsza wartość to
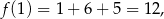
a największa to
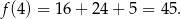
Na koniec obrazek.
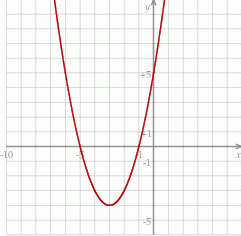
Odpowiedź: 
