Zadanie nr 1078650
Zbadaj zbieżność całki niewłaściwej 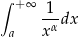 dla
dla 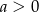 .
.
Rozwiązanie
Niech 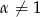 . Wtedy
. Wtedy
![∫ + ∞ ∫ +∞ [ ]+∞ [ ]+∞ 1-dx = x −αdx = ---1----x−α+ 1 = ---1---⋅ --1-- . a xα a − α + 1 a − α+ 1 xα−1 a](https://img.zadania.info/zad/1078650/HzadR1x.gif)
Ostatnia granica jest równa 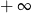 gdy
gdy 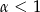 , lub jest równa liczbie skończonej:
, lub jest równa liczbie skończonej: 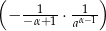 gdy
gdy 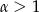 .
.
Dla 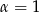 mamy
mamy
![∫ ∞ 1 +∞ xdx = [ln x]a = + ∞ . a](https://img.zadania.info/zad/1078650/HzadR7x.gif)
Tak więc całka niewłaściwa 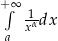 jest zbieżna dla
jest zbieżna dla 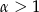 , a rozbieżna dla
, a rozbieżna dla 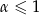 .
.
Odpowiedź: Zbieżna dla 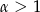 , a rozbieżna dla
, a rozbieżna dla