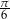Zadanie nr 2101805
Oblicz całkę 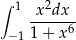 .
.
Rozwiązanie
Sposób I
Ponieważ całkujemy funkcję parzystą mamy
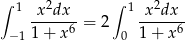
Podstawiamy 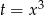 . Wtedy
. Wtedy 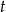 zmienia się w przedziale
zmienia się w przedziale ![[0,1]](https://img.zadania.info/zad/2101805/HzadR3x.gif) oraz
oraz
![∫ 1 2 || 3 || ∫ 1 2 x--dx--= | t = x | = 2- --dt-- = 0 1+ x6 |dt = 3x2dx| 3 0 1 + t2 2 2 (π ) π = --[a rc tg t]10 = -- -- − 0 = --. 3 3 4 6](https://img.zadania.info/zad/2101805/HzadR4x.gif)
Sposób II
Tak jak poprzednio podstawiamy 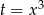 , ale robimy to w oryginalnej całce.
, ale robimy to w oryginalnej całce.
![∫ 1 x2dx || 3 || 1 ∫ 1 dt -------= || t = x2 || = -- ------ = −1 1 + x6 dt = 3x dx 3 −1 1 + t2 1 1 1( π π ) π = -[arctgt]−1 = -- --+ -- = --. 3 3 4 4 6](https://img.zadania.info/zad/2101805/HzadR6x.gif)
Odpowiedź: 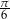
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 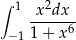 .
.
Sposób I
Ponieważ całkujemy funkcję parzystą mamy
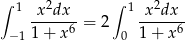
Podstawiamy 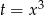 . Wtedy
. Wtedy 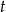 zmienia się w przedziale
zmienia się w przedziale ![[0,1]](https://img.zadania.info/zad/2101805/HzadR3x.gif) oraz
oraz
![∫ 1 2 || 3 || ∫ 1 2 x--dx--= | t = x | = 2- --dt-- = 0 1+ x6 |dt = 3x2dx| 3 0 1 + t2 2 2 (π ) π = --[a rc tg t]10 = -- -- − 0 = --. 3 3 4 6](https://img.zadania.info/zad/2101805/HzadR4x.gif)
Sposób II
Tak jak poprzednio podstawiamy 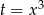 , ale robimy to w oryginalnej całce.
, ale robimy to w oryginalnej całce.
![∫ 1 x2dx || 3 || 1 ∫ 1 dt -------= || t = x2 || = -- ------ = −1 1 + x6 dt = 3x dx 3 −1 1 + t2 1 1 1( π π ) π = -[arctgt]−1 = -- --+ -- = --. 3 3 4 4 6](https://img.zadania.info/zad/2101805/HzadR6x.gif)
Odpowiedź: