Zadanie nr 2355705
Oblicz całkę 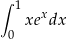 .
.
Rozwiązanie
Sposób I
Całkujemy przez części.
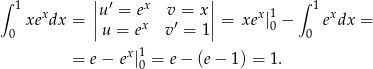
Sposób II
Liczymy najpierw całkę nieoznaczoną (przez części).
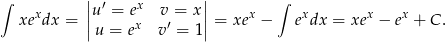
Liczymy teraz całkę oznaczoną.
![∫ 1 x x x 1 xe dx = [xe − e ]0 = 0 − (− 1) = 1. 0](https://img.zadania.info/zad/2355705/HzadR2x.gif)
Odpowiedź: 1
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 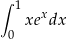 .
.
Sposób I
Całkujemy przez części.
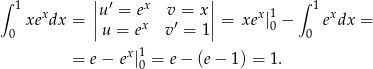
Sposób II
Liczymy najpierw całkę nieoznaczoną (przez części).
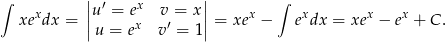
Liczymy teraz całkę oznaczoną.
![∫ 1 x x x 1 xe dx = [xe − e ]0 = 0 − (− 1) = 1. 0](https://img.zadania.info/zad/2355705/HzadR2x.gif)
Odpowiedź: 1
