Zadanie nr 2456992
Oblicz całkę 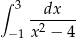 .
.
Rozwiązanie
Liczymy najpierw funkcję pierwotną.
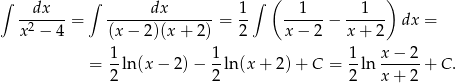
Zatem
![∫ 3 ∫ 2 ∫ 3 [ ] 2 [ ]3 --dx---= -dx---+ --dx--- = ln x-−-2- + ln x−--2- . −1 x2 − 4 −1 x2 − 4 2 x 2 − 4 x + 2 −1 x+ 2 2](https://img.zadania.info/zad/2456992/HzadR1x.gif)
Ponieważ
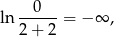
więc całka jest rozbieżna.
Odpowiedź: Rozbieżna
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 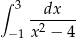 .
.
Liczymy najpierw funkcję pierwotną.
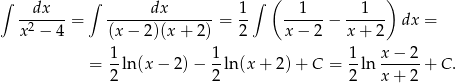
Zatem
![∫ 3 ∫ 2 ∫ 3 [ ] 2 [ ]3 --dx---= -dx---+ --dx--- = ln x-−-2- + ln x−--2- . −1 x2 − 4 −1 x2 − 4 2 x 2 − 4 x + 2 −1 x+ 2 2](https://img.zadania.info/zad/2456992/HzadR1x.gif)
Ponieważ
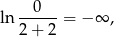
więc całka jest rozbieżna.
Odpowiedź: Rozbieżna
