/Studia/Analiza/Całki oznaczone

Zadanie nr 2947866

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę niewłaściwą 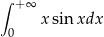∫ +∞ x sin xdx 0 .

Rozwiązanie

Wyznaczymy funkcję pierwotną całkując przez części.

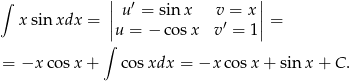
∫ || u′ = sinx v = x || xsin xdx = || ′ || = ∫ u = − cosx v = 1 = −x cosx + cosxdx = −x cosx + sin x + C.

Za funkcję pierwotną możemy więc przyjąć 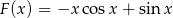F(x) = −x cos x+ sin x .

Mamy 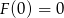F(0) = 0 , natomiast granica

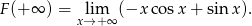
F(+ ∞ ) = lim (−x co sx + sinx ). x→ +∞

nie istnieje (łatwo to wykazać za pomocą definicji Heinego granicy funkcji, rozpatrując dwa ciągi 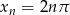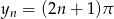xn = 2n π , yn = (2n + 1 )π ). Zatem całka 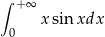∫ + ∞ xsin xdx 0 jest rozbieżna.  
Odpowiedź: Rozbieżna

Wersja PDF