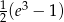Zadanie nr 4415752
Oblicz całkę 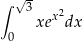 .
.
Rozwiązanie
Podstawiamy 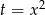 . Wtedy
. Wtedy 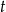 zmienia się w przedziale
zmienia się w przedziale ![[0 ,3]](https://img.zadania.info/zad/4415752/HzadR2x.gif) .
.
![∫ √ 3 || 2 || ∫ 3 [ ] xex2dx = | t = x |= 1- etdt = 1- et 3= 1-(e3 − 1). 0 |dt = 2xdx | 2 0 2 0 2](https://img.zadania.info/zad/4415752/HzadR3x.gif)
Odpowiedź: 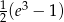
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 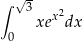 .
.
Podstawiamy 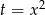 . Wtedy
. Wtedy 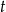 zmienia się w przedziale
zmienia się w przedziale ![[0 ,3]](https://img.zadania.info/zad/4415752/HzadR2x.gif) .
.
![∫ √ 3 || 2 || ∫ 3 [ ] xex2dx = | t = x |= 1- etdt = 1- et 3= 1-(e3 − 1). 0 |dt = 2xdx | 2 0 2 0 2](https://img.zadania.info/zad/4415752/HzadR3x.gif)
Odpowiedź: