Zadanie nr 5132327
Oblicz całkę 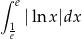 .
.
Rozwiązanie
Rozbijamy przedział całkowania tak, aby pozbyć się wartości bezwzględnej.
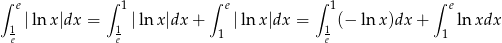
Obliczmy teraz całkę nieoznaczoną 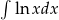 . Całkujemy przez części.
. Całkujemy przez części.
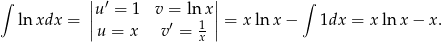
Mamy więc
![∫ ∫ ∫ e 1 e 1 e 1 |ln x|dx = 1 (− lnx )dx+ 1 lnxdx = [x(1 − ln x)]1e + [x (ln x − 1)]1 = e( ) e = 1− 2- + (0+ 1) = 2 − 2-. e e](https://img.zadania.info/zad/5132327/HzadR3x.gif)
Odpowiedź: 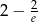
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 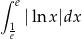 .
.
Rozbijamy przedział całkowania tak, aby pozbyć się wartości bezwzględnej.
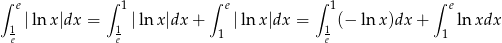
Obliczmy teraz całkę nieoznaczoną 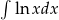 . Całkujemy przez części.
. Całkujemy przez części.
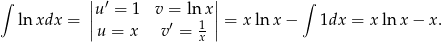
Mamy więc
![∫ ∫ ∫ e 1 e 1 e 1 |ln x|dx = 1 (− lnx )dx+ 1 lnxdx = [x(1 − ln x)]1e + [x (ln x − 1)]1 = e( ) e = 1− 2- + (0+ 1) = 2 − 2-. e e](https://img.zadania.info/zad/5132327/HzadR3x.gif)
Odpowiedź: