/Studia/Analiza/Całki oznaczone

Zadanie nr 5438782

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę niewłaściwą 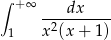∫ +∞ dx -2-------- 1 x (x + 1 )

Rozwiązanie

Najpierw obliczymy funkcję pierwotną, czyli całkę nieoznaczoną. Ponieważ mamy do czynienia z funkcją wymierną, więc znajdujemy rozkład na ułamki proste.

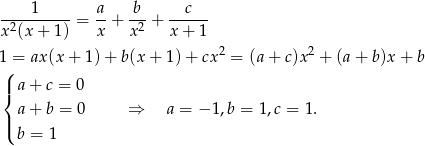
----1-----= a-+ b--+ --c--- x2(x + 1 ) x x2 x + 1 2 2 1( = ax (x+ 1)+ b(x+ 1)+ cx = (a + c)x + (a+ b)x + b | a + c = 0 { | a + b = 0 ⇒ a = − 1,b = 1,c = 1. ( b = 1

Stąd

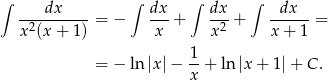
∫ dx ∫ dx ∫ dx ∫ dx -2--------= − ---+ --2 + ------ = x (x + 1 ) x x x + 1 1- = − ln |x |− x + ln |x+ 1|+ C.

Zatem funkcja podcałkowa ma w przedziale 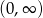(0,∞ ) funkcję pierwotną

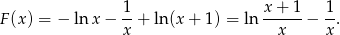
F(x) = − ln x − -1+ ln (x+ 1) = ln x+--1-− 1-. x x x

Mamy

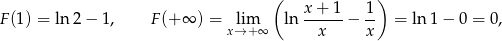
( x + 1 1) F(1) = ln 2− 1, F (+ ∞ ) = lim ln ------− -- = ln1 − 0 = 0, x→+ ∞ x x

skąd

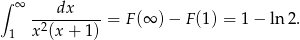
∫ ∞ ---dx----- 1 x2(x + 1) = F(∞ )− F(1) = 1 − ln 2.

 
Odpowiedź: 1 − ln2

Wersja PDF