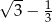Zadanie nr 8825905
Oblicz całkę 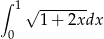 .
.
Rozwiązanie
Sposób I
Liczymy najpierw całkę nieoznaczoną (przez podstawienie).
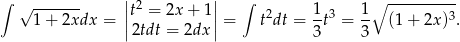
Teraz obliczamy całkę oznaczoną
![∫ 1√ ------- 1[ ∘ ---------]1 1 √ --- √ -- 1 1 + 2xdx = -- (1+ 2x)3 = -( 27 − 1) = 3− -- 0 3 0 3 3](https://img.zadania.info/zad/8825905/HzadR1x.gif)
Sposób II
Jak poprzednio podstawiamy 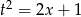 . Aby obliczyć nowe granice całkowania, wstawiamy
. Aby obliczyć nowe granice całkowania, wstawiamy 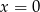 i
i 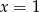 do wzoru
do wzoru 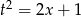 . Aby móc jednoznacznie wyliczyć
. Aby móc jednoznacznie wyliczyć 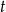 , możemy dodatkowo założyć, że
, możemy dodatkowo założyć, że 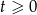 , czyli po zmianie zmiennej będziemy całkować w przedziale
, czyli po zmianie zmiennej będziemy całkować w przedziale ![√ -- [0, 3]](https://img.zadania.info/zad/8825905/HzadR8x.gif) . Mamy zatem
. Mamy zatem
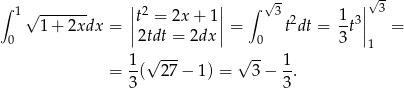
Odpowiedź: