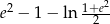Zadanie nr 9722959
Oblicz całkę 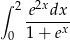 .
.
Rozwiązanie
Podstawiamy 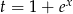 . Wtedy
. Wtedy 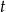 zmienia się w przedziale
zmienia się w przedziale ![2 [2,1 + e ]](https://img.zadania.info/zad/9722959/HzadR2x.gif) .
.
![∫ 2 x x || x|| ∫ 1+e2 ∫ 1+e 2( ) e--⋅e-dx-= |t = 1+x e |= (t-−-1)dt = 1− 1- dt = 0 1 + ex |dt = e dx | 2 t 2 t 2 1+ e2 = [t− ln t]1+2e = 1+ e2 − ln(1 + e2)− 2+ ln 2 = e2 − 1 − ln ------. 2](https://img.zadania.info/zad/9722959/HzadR3x.gif)
Odpowiedź: 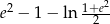
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 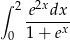 .
.
Podstawiamy 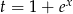 . Wtedy
. Wtedy 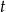 zmienia się w przedziale
zmienia się w przedziale ![2 [2,1 + e ]](https://img.zadania.info/zad/9722959/HzadR2x.gif) .
.
![∫ 2 x x || x|| ∫ 1+e2 ∫ 1+e 2( ) e--⋅e-dx-= |t = 1+x e |= (t-−-1)dt = 1− 1- dt = 0 1 + ex |dt = e dx | 2 t 2 t 2 1+ e2 = [t− ln t]1+2e = 1+ e2 − ln(1 + e2)− 2+ ln 2 = e2 − 1 − ln ------. 2](https://img.zadania.info/zad/9722959/HzadR3x.gif)
Odpowiedź: