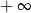Zadanie nr 9756235
Oblicz całkę 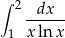 .
.
Rozwiązanie
Funkcja podcałkowa ma w przedziale ![[1,2]](https://img.zadania.info/zad/9756235/HzadR0x.gif) jeden punkt osobliwy
jeden punkt osobliwy 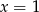 . Całkujemy podstawiając
. Całkujemy podstawiając 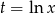 . Liczymy całkę nieoznaczoną
. Liczymy całkę nieoznaczoną
![∫ 2 || || ∫ ln 2 --dx--= |t = lnx |= dt-= [ln t]ln2 = ln ln 2− (− ∞ ) = + ∞ . 1 x lnx |dt = dxx-| 0 t 0](https://img.zadania.info/zad/9756235/HzadR3x.gif)
Odpowiedź: 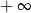
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 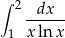 .
.
Funkcja podcałkowa ma w przedziale ![[1,2]](https://img.zadania.info/zad/9756235/HzadR0x.gif) jeden punkt osobliwy
jeden punkt osobliwy 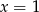 . Całkujemy podstawiając
. Całkujemy podstawiając 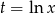 . Liczymy całkę nieoznaczoną
. Liczymy całkę nieoznaczoną
![∫ 2 || || ∫ ln 2 --dx--= |t = lnx |= dt-= [ln t]ln2 = ln ln 2− (− ∞ ) = + ∞ . 1 x lnx |dt = dxx-| 0 t 0](https://img.zadania.info/zad/9756235/HzadR3x.gif)
Odpowiedź: