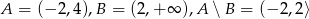/Szkoła średnia/Nierówności/Układy nierówności/Różne

Zadanie nr 3115141

Wyznacz zbiory:

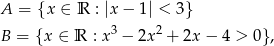
A = {x ∈ R : |x − 1| < 3} B = {x ∈ R : x3 − 2x2 + 2x − 4 > 0},

a następnie wyznacz zbiór A ∖ B .

Wersja PDF

Rozwiązanie

Rozwiązujemy pierwszą nierówność

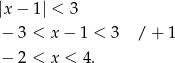
|x− 1| < 3 − 3 < x − 1 < 3 / + 1 − 2 < x < 4 .

Aby rozwiązać drugą nierówność, musimy rozłożyć podany wielomian na czynniki. Sprawdzając dzielniki wyrazu wolnego, łatwo znaleźć pierwiastek 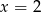x = 2 . Dzielimy zatem wielomian przez 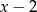x − 2 . My zrobimy to grupując wyrazy.

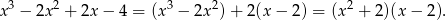
x 3 − 2x 2 + 2x− 4 = (x3 − 2x2) + 2(x − 2 ) = (x2 + 2)(x− 2).

Zatem 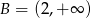B = (2,+ ∞ ) oraz

A ∖ B = (− 2,2 ⟩.

 
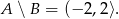
Odpowiedź: A = (− 2,4),B = (2,+ ∞ ),A ∖ B = (− 2,2⟩

Wersja PDF