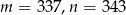/Szkoła średnia/Nierówności/Układy nierówności/Różne

Zadanie nr 5332915

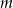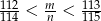Podaj przykład dwóch liczb naturalnych m i n , które spełniają nierówność 111124 < mn-< 111315- .

Wersja PDF

Rozwiązanie

Sposób I

Sprowadźmy oba skrajne ułamki do wspólnego mianownika.

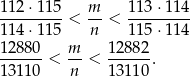
112 ⋅115 m 113⋅ 114 ---------< -- < --------- 114 ⋅115 n 115⋅ 114 1288-0 < m- < 12882-. 1311 0 n 13110

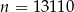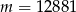Widać teraz, że możemy wziąć n = 1 3110 i m = 128 81 .

Sposób II

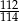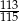Możemy wziąć środek odcinka o końcach 112 114 i 113 115 . Z pewnością będzie to liczba wymierna i będzie spełniała żądaną nierówność. Liczymy

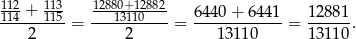
112 113 12880+12882 114 +-115= ---13110--- = 64-40+--6441 = 12881-. 2 2 1 3110 13110

Sposób III

Nierówność z treści zadania można zapisać w postaci

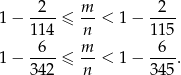
2 m 2 1− 114-≤ n-< 1 − 115- 6 m 6 1− ----≤ --< 1 − ----. 342 n 345

Widać teraz, że można np wziąć

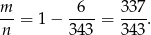
m 6 337 --= 1 − ----= ----. n 343 343

 
Odpowiedź: Np. 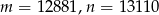m = 12881,n = 13110 lub m = 33 7,n = 343

Wersja PDF