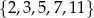Zadanie nr 8399513
Wyznacz wszystkie liczby pierwsze, które należą do zbioru 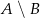 , gdzie
, gdzie 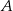 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
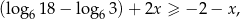
a 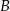 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
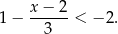
Rozwiązanie
Rozwiązujemy pierwszą nierówność
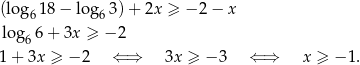
Zatem 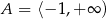 .
.
Rozwiązujemy teraz drugą nierówność
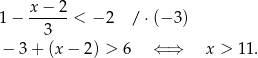
Zatem 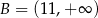 i
i
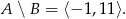
Liczby pierwsze w tym przedziale to
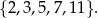
Odpowiedź: