Zadanie nr 5446397
Wykaż, że jeżeli promień okręgu opisanego na trójkącie równoramiennym jest dwa razy dłuższy od promienia okręgu wpisanego w ten trójkąt, to trójkąt ten jest równoboczny.
Rozwiązanie
Szkicujemy trójkąt równoramienny.
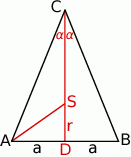
Niech 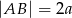 i
i 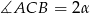 . Na mocy twierdzenia sinusów mamy
. Na mocy twierdzenia sinusów mamy
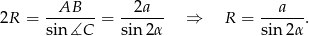
Sposób I
Z trójkąta prostokątnego  mamy
mamy
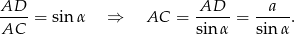
Promień  okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt  obliczamy ze wzoru na pole
obliczamy ze wzoru na pole 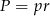 , gdzie
, gdzie
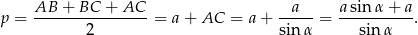
jest połową obwodu trójkąta. Mamy zatem
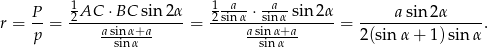
Mamy więc równanie
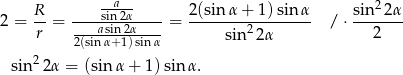
Korzystamy teraz ze wzoru na 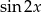 oraz z tego, że
oraz z tego, że 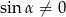 i
i 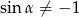 .
.
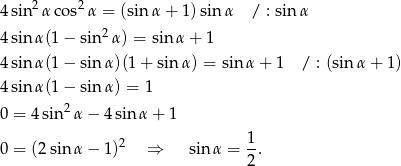
Stąd 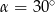 , czyli
, czyli 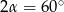 , a to oznacza, że trójkąt
, a to oznacza, że trójkąt 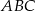 jest równoboczny.
jest równoboczny.
Sposób II
Tym razem promień okręgu wpisanego obliczymy z trójkąta 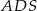 , gdzie
, gdzie 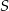 jest środkiem okręgu wpisanego. Zauważmy najpierw, że
jest środkiem okręgu wpisanego. Zauważmy najpierw, że
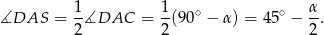
Mamy zatem
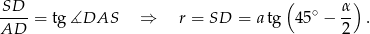
Przekształćmy trochę otrzymane wyrażenie na promień – korzystamy ze wzorów na sinus/cosinus różnicy.
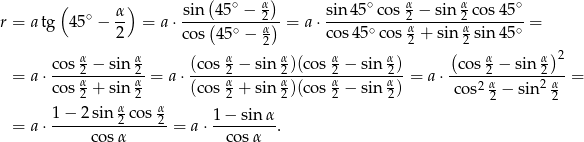
Musimy więc rozwiązać równanie
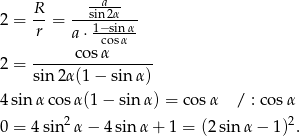
Stąd 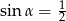 , czyli
, czyli 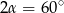 , co oznacza, że trójkąt
, co oznacza, że trójkąt 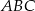 jest równoboczny.
jest równoboczny.

