/Szkoła podstawowa/Zadania z treścią/Różne

Zadanie nr 5575034

Rozmieniono 34 złote na 116 monet, wśród których były tylko monety 50 i 20 groszowe. Ile było monet 50 groszowych?

Wersja PDF

Rozwiązanie

Sposób I

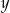Jeżeli oznaczymy przez x i y liczby monet 50 i 20 groszowych odpowiednio, to mamy układ równań

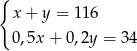
{ x + y = 116 0,5x + 0,2y = 34

Podstawiamy 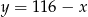y = 116 − x do drugiego równania

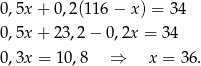
0,5x + 0,2(116 − x) = 3 4 0,5x + 23,2− 0,2x = 3 4 0,3x = 10,8 ⇒ x = 36.

Sposób II

Gdybyśmy rozmienili wszystko na 50-groszówki to byłoby ich 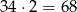34⋅ 2 = 68 , czyli brakuje 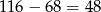1 16− 68 = 48 monet. Zauważmy, że zamiana złotówki rozmienionej na 50-ki na złotówkę rozmienioną na 20-ki zwiększa liczbę monet o 3. W takim razie musimy to zrobić 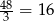48 = 16 3 razy. Zatem na 50-ki jest rozmienionych 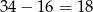34 − 16 = 18 złotówek.  
Odpowiedź: 36

Wersja PDF