/Szkoła podstawowa/Zadania z treścią/Różne

Zadanie nr 5923175

Chłopiec ma monety po 50 gr i po 20 gr, razem 27 sztuk. Monety mają łączną wartość 8,70 zł. Ile monet po 50 gr, a ile po 20 gr ma chłopiec?

Wersja PDF

Rozwiązanie

Sposób I

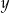Jeżeli oznaczymy przez x i y ilości monet 50 gr i 20 gr to mamy układ równań

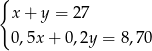
{ x + y = 27 0,5x + 0 ,2y = 8,70

Odejmując od pierwszego równania dwa razy drugie (żeby skrócić x ) mamy

y − 0,4y = 28 − 17,4 ⇒ 0 ,6y = 9,6 ⇒ y = 16.

Zatem x = 1 1 .

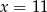Sposób II

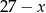Mogliśmy też od razu ułożyć równanie z jedną niewiadomą. Jeżeli x oznacza liczbę 50 groszówek, to 20 groszówek jest 2 7− x i mamy równanie

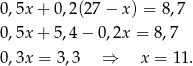
0,5x + 0,2(27 − x ) = 8,7 0,5x + 5,4 − 0,2x = 8,7 0,3x = 3 ,3 ⇒ x = 11 .

Zatem 20 groszówek jest 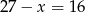27 − x = 16 .  
Odpowiedź: 11 po 50 gr i 16 po 20 gr

Wersja PDF