/Szkoła podstawowa/Zadania z treścią/Waga

Zadanie nr 9477989

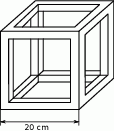
Wojtek wykonał taki model sześcianu, jak przedstawiono na rysunku. Używał listewek, których przekrój poprzeczny jest kwadratem o boku 2 cm. Krawędź sześcianu ma długość 20 cm. Oblicz masę tego modelu, wiedząc, że 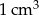1 cm 3 drewna, z którego go wykonano, ma masę 0,8 g. Zapisz obliczenia.

PIC

Wersja PDF

Rozwiązanie

Sposób I

Podzielmy listewki, z których zbudowany jest model na małe sześcianiki o krawędzi 2.

PIC

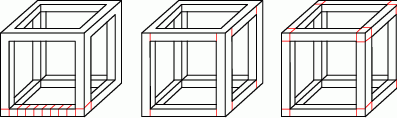
Policzmy ile jest takich sześcianików: jest ich 8 w narożnikach, oraz po 8 na każdej krawędzi. Ponieważ jest 12 krawędzi jest

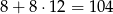
8 + 8 ⋅12 = 10 4

takich sześcianików. Objętość tego modelu jest więc równa

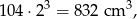
3 3 104⋅ 2 = 832 cm ,

a jego masa wynosi

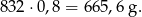
83 2⋅0,8 = 665,6 g.

Sposób II

Tym razem podzielmy model na cztery pionowe prostopadłościany (pionowe krawędzie) o wysokości 20 cm, oraz 8 poziomych krawędzi o długości 16. Objętość jest więc równa

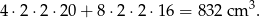
3 4 ⋅2 ⋅2⋅2 0+ 8 ⋅2 ⋅2 ⋅16 = 832 cm .

Masa modelu wynosi:

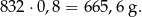
83 2⋅0,8 = 665,6 g.

Sposób III

Podzielmy sześcian na 8 narożników (czyli sześcianów o krawędzi 2), oraz 12 prostopadłościanów w krawędziach. Prostopadłościany te mają wymiary 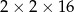2 × 2 × 16 . Objętość modelu jest więc równa

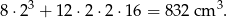
8 ⋅23 + 12 ⋅2 ⋅2⋅1 6 = 832 cm 3.

Masa modelu wynosi:

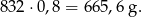
83 2⋅0,8 = 665,6 g.

Sposób IV

Tym razem zastanówmy się jak otrzymać opisany model z pełnego sześcianu o krawędzi długości 20 cm. Najpierw musimy wyciąć ze środka mniejszy sześcian o krawędzi długości 16. Potem z każdej ściany musimy wyciąć kwadrat (prostopadłościan) o wymiarach 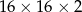16× 16 × 2 . Objętość modelu jest więc równa

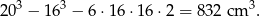
20 3 − 16 3 − 6 ⋅16 ⋅16 ⋅2 = 832 cm 3.

Masa modelu wynosi:

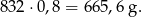
83 2⋅0,8 = 665,6 g.

 
Odpowiedź: 665,6 g

Wersja PDF