/Szkoła podstawowa/Zadania z treścią/Liczby

Zadanie nr 4562770

Kod dostępu do komputera Andrzeja złożony jest z czterech kolejnych wielokrotności liczby 7 ustawionych od najmniejszej do największej. Suma tych wielokrotności wynosi 294. Znajdź liczby, z których złożony jest ten kod. Zapisz swoje rozumowanie.

Wersja PDF

Rozwiązanie

Sposób I

Ponieważ

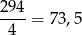
2 94 ---- = 73 ,5 4

szukane liczby muszą być w okolicy liczby 73,5. Sąsiednie liczby podzielne przez 7 to (bierzemy dwie mniejsze i dwie większe)

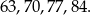
63,70,77,8 4.

Wystarczy teraz sprawdzić, że

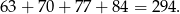
63+ 70+ 77 + 84 = 29 4.

Sposób II

Skoro szukamy kolejnych liczb naturalnych podzielnych przez 7, to możemy oznaczyć szukane liczby przez 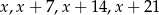x,x + 7 ,x+ 14,x + 21 . Otrzymujemy równanie

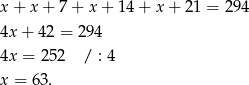
x + x + 7 + x + 14 + x + 21 = 294 4x + 42 = 294 4x = 2 52 / : 4 x = 63 .

Zatem szukane liczby to: 63, 70, 77, 84.

Sposób III

Skoro szukamy kolejnych liczb naturalnych podzielnych przez 7, to możemy oznaczyć szukane liczby przez 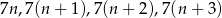7n,7 (n + 1),7(n + 2),7(n + 3) . Otrzymujemy równanie

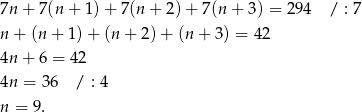
7n + 7(n+ 1)+ 7(n + 2) + 7(n + 3) = 2 94 / : 7 n + (n + 1)+ (n + 2)+ (n + 3) = 42 4n + 6 = 42 4n = 36 / : 4 n = 9.

Zatem szukane liczby to: 63, 70, 77, 84.  
Odpowiedź: 63, 70, 77, 84

Wersja PDF