Zadanie nr 5761482
Wykaż, że dla dowolnej liczby całkowitej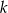 
różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od 
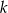jest równa -2.
Rozwiązanie
Jedyna trudność w tym zadaniu to zapisanie przy pomocy symboli zagmatwanej tezy, którą mamy uzasadnić. Musimy pokazać, że wyrażenie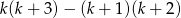 
jest równe -2. Liczymy
