/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Różne

Zadanie nr 8529738

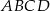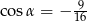Dany jest czworokąt ABCD , którego kolejne boki mają długości 4,5,7,8. Kat między najkrótszymi bokami ma miarę α , taką że cos α = − 196 . Sprawdź czy na tym czworokącie można opisać okrąg.

Wersja PDF

Rozwiązanie

Przyjmijmy oznaczenia z rysunku.

PIC

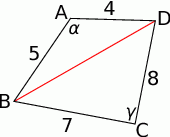
Musmy sprawdzić czy 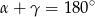α + γ = 180∘ , czyli czy

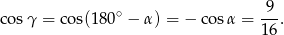
cosγ = cos(180∘ − α ) = − cos α = -9-. 16

Zrobimy to korzystając z twierdzenia cosinusów w trójkącie 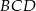BCD , ale najpierw musimy wyliczyć 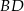BD z trójkąta ABD .

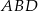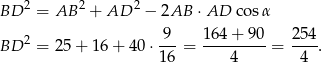
2 2 2 BD = AB + AD − 2AB ⋅AD cos α 2 9 164 + 90 254 BD = 2 5+ 16+ 40⋅ ---= ---------= ---. 16 4 4

Teraz stosujemy twierdzenie cosinusów w trójkacie BCD .

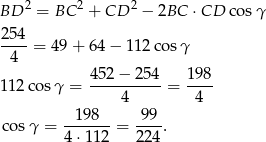
BD 2 = BC 2 + CD 2 − 2BC ⋅CD cos γ 254-= 49 + 64 − 112 cosγ 4 452-−-25-4 19-8 112 cosγ = 4 = 4 198 99 cos γ = -------= ----. 4⋅1 12 2 24

Zatem na czworokącie nie można opisać okręgu.  
Odpowiedź: Nie, nie można

Wersja PDF