Zadanie nr 2889948
Dla jakich wartości parametrów  i
i 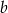 punkt
punkt 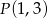 jest punktem przegięcia krzywej
jest punktem przegięcia krzywej 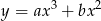 ?
?
Rozwiązanie
Po pierwsze ten punkt musi leżeć na krzywej:
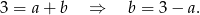
Mamy zatem krzywą
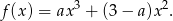
Punkt 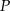 będzie punktem przegięcia jeżeli
będzie punktem przegięcia jeżeli 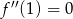 , oraz druga pochodna musi zmieniać znak przechodząc przez
, oraz druga pochodna musi zmieniać znak przechodząc przez 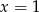 . Liczymy
. Liczymy
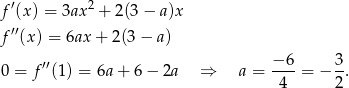
Stąd
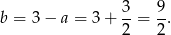
Mamy zatem krzywą
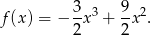
Odpowiedź: