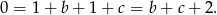/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Udowodnij...

Zadanie nr 4972388

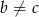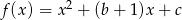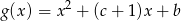Wykaż że jeśli b ⁄= c i funkcje kwadratowe 2 f(x) = x + (b+ 1)x+ c oraz g (x ) = x2 + (c+ 1)x + b mają wspólne miejsce zerowe, to b + c + 2 = 0 .

Wersja PDF

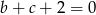Rozwiązanie

Jeżeli 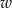w jest wspólnym miejscem zerowym to mamy

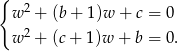
{ 2 w + (b+ 1)w + c = 0 w 2 + (c+ 1)w + b = 0.

Odejmując od pierwszego równania drugie (żeby skrócić 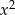x2 ) mamy

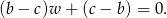
(b − c)w + (c− b) = 0.

Ponieważ 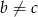b ⁄= c daje to nam.

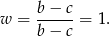
b− c w = -----= 1. b− c

Wstawiając 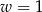w = 1 do któregokolwiek z równań mamy

0 = 1 + b + 1 + c = b + c + 2.
Wersja PDF