/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Udowodnij...

Zadanie nr 5948277

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że dla dowolnej liczby całkowitej 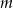m rozwiązania równania 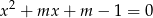x 2 + mx + m − 1 = 0 z niewiadomą x są liczbami całkowitymi.

Rozwiązanie

Sposób I

Spróbujmy rozwiązać podane równanie,

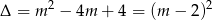
2 2 Δ = m − 4m + 4 = (m − 2 )

Zatem 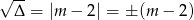√ -- Δ = |m − 2| = ± (m − 2) i pierwiastki są równe

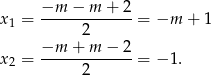
−m − m + 2 x 1 = -------------= −m + 1 2 −m--+--m-−-2- x 2 = 2 = − 1.

Widać, że każdy z tych pierwiastków jest liczbą całkowitą.

Sposób II

Zamiast liczyć 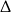Δ -ę spróbujmy rozwiązanie równanie bezpośrednio – grupując wyrazy.

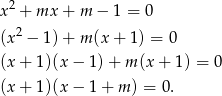
2 x + mx + m − 1 = 0 (x2 − 1)+ m(x + 1) = 0 (x+ 1)(x − 1) + m (x+ 1) = 0 (x+ 1)(x − 1 + m ) = 0.

Widać, że oba pierwiastki są całkowite.

Wersja PDF