/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Udowodnij...

Zadanie nr 8329451

Wykaż, że dla dowolnej liczby rzeczywistej 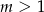m > 1 istnieje dokładnie jedna liczba rzeczywista x taka, że

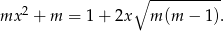
∘ ---------- mx 2 + m = 1 + 2x m (m − 1).
Wersja PDF

Rozwiązanie

Sposób I

Jeżeli zapiszemy dane równanie w postaci

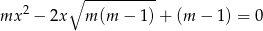
∘ ---------- mx 2 − 2x m(m − 1) + (m − 1) = 0

to widać, że mamy do czynienia ze zwykłym równaniem kwadratowym. Liczymy 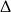Δ -ę.

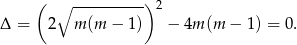
( ∘ ---------) 2 Δ = 2 m(m − 1) − 4m (m − 1) = 0.

To oznacza, że powyższe równanie kwadratowe ma zawsze jedno rozwiązanie.

Sposób II

Przekształcamy dane równanie w sposób równoważny.

2 ∘ ---------- mx − 2x m (m − 1) + (m − 1) = 0 √ -- ∘ ---------- ∘ --------- ( mx )2 − 2x m (m − 1) + (m − 1)2 = 0 (√ -- √ ------)2 mx − m − 1 = 0 √ -- √ ------ mx − m − 1 = 0 √ ------ --m-−--1 x = √ m .
Wersja PDF