Zadanie nr 9918699
Suma pierwiastków trójmianu 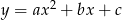 jest równa
jest równa 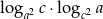 , gdzie
, gdzie 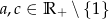 . Uzasadnij, że odcięta wierzchołka paraboli będącej wykresem tego trójmianu jest równa
. Uzasadnij, że odcięta wierzchołka paraboli będącej wykresem tego trójmianu jest równa  .
.
Rozwiązanie
Przekształćmy najpierw podane wyrażenie
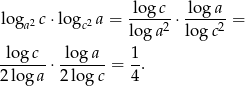
Na mocy wzorów Viète’a mamy zatem
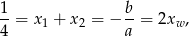
gdzie 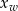 oznacza pierwszą współrzędną wierzchołka paraboli. Stąd
oznacza pierwszą współrzędną wierzchołka paraboli. Stąd 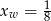 .
.

