Zadanie nr 1176929
W trójkącie 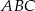 prowadzimy dwusieczną kąta
prowadzimy dwusieczną kąta 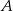 i przez punkt
i przez punkt 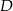 przecięcia się tej dwusiecznej z bokiem
przecięcia się tej dwusiecznej z bokiem 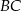 prowadzimy proste równoległe do boków
prowadzimy proste równoległe do boków 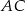 i
i 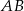 , które przecinają te boki odpowiednio w punktach
, które przecinają te boki odpowiednio w punktach 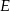 i
i 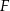 . Wykaż, że czworokąt
. Wykaż, że czworokąt 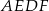 jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
Rozwiązanie
Narysujmy opisaną sytuację.
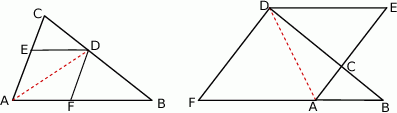
Z podanych informacji wynika, że czworokąt 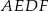 jest równoległobokiem. Ponadto jego przekątna jest jednocześnie dwusieczną jego kąta wewnętrznego. Równoległobok o tej własności musi być rombem (bo wtedy trójkąty
jest równoległobokiem. Ponadto jego przekątna jest jednocześnie dwusieczną jego kąta wewnętrznego. Równoległobok o tej własności musi być rombem (bo wtedy trójkąty 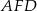 i
i 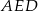 są równoramienne).
są równoramienne).
Analogiczna sytuacja dla dwusiecznej kąta zewnętrznego przedstawiona jest na prawym rysunku.

