/Szkoła podstawowa/Geometria

Zadanie nr 2831980

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz objętość graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 16 cm i 30 cm, a krawędź boczna jest dwa razy dłuższa od krawędzi podstawy.

Rozwiązanie

Zaczynamy od rysunku.

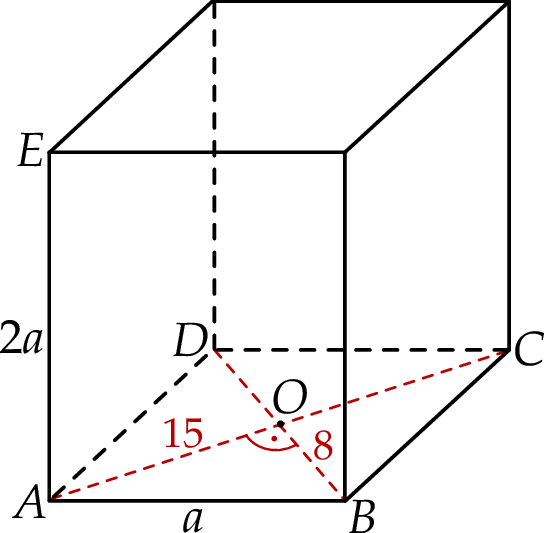
ZINFO-FIGURE

Ponieważ przekątne rombu są prostopadłe i dzielą się na połowy, jego bok jest równy

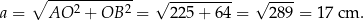
∘ ------------ √ --------- √ ---- a = AO 2 + OB 2 = 22 5+ 64 = 289 = 17 cm .

Wysokość graniastosłupa jest więc równa 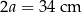2a = 34 cm . Obliczmy jeszcze pole rombu w podstawie

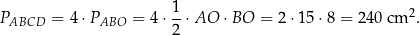
1 PABCD = 4⋅PABO = 4⋅ --⋅AO ⋅BO = 2 ⋅15 ⋅8 = 2 40 cm 2. 2

Objętość graniastosłupa jest więc równa

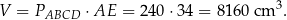
V = PABCD ⋅AE = 240 ⋅34 = 816 0 cm 3.

 
Odpowiedź: V = 816 0 cm 3

Wersja PDF