Zadanie nr 3123270
Z czterech ołowianych sześcianów o przekątnej długości 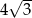 wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
Rozwiązanie
Przekątna sześcianu o krawędzi długości  ma długość
ma długość 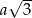 (można to łatwo wyliczyć z twierdzenia Pitagorasa). Mamy zatem równanie
(można to łatwo wyliczyć z twierdzenia Pitagorasa). Mamy zatem równanie
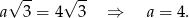
Tak więc dane sześciany mają krawędź długości 4 i opisany graniastosłup powstaje przez sklejenie wszystkich czterech sześcianów tak, aby miały wspólną krawędź.
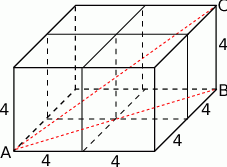
Długość przekątnej 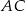 tego prostopadłościanu możemy obliczyć z trójkąta prostokątnego
tego prostopadłościanu możemy obliczyć z trójkąta prostokątnego 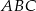
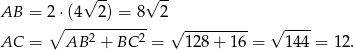
Odpowiedź: 12

